کلمات کلیدی: الگوی علّی، مفاهیم مقدار، ارزش، مفهوم شناسی
مثال: «انسان» دو حالت دارد: زن، مرد. البته این دو حالت به لحاظ جنسیت است. میتوان به لحاظ تقوا حالتهای متعددی برای انسان در نظر گرفت. مثال: «میوه» انواع (حالت های) متعددی دارد: سیب، گلابی، گیلاس، و … یک فرد ممکن است سیب را به گلابی ترجیح دهد و فرد دیگری گلابی را به سیب ترجیح دهد.
فردی که حالتها را رجحانبندی میکند، مرجع ارزش نامیده میشود. یک حالت ممکن است از دید افراد مختلف (مراجع ارزش مختلف) ارزشهای متفاوتی داشته باشد. اما یک حالت، از نظر یک مرجع ارزش در یک زمان تنها میتواند یک ارزش داشته باشد. به عبارت دیگر رابطه بین ارزشها و حالتهای یک شی دارای مشخصات تابع (به مفهوم ریاضی) است. مجموعه حالتها، دامنه و مجموعه ارزشها، برد این تابع هستند. تابع ارزش مفهومی کارا است اما معمولاً به طور دقیق نمیتوان آن را مشخص نمود.
هر یک از ارزشهای یک شی ممکن است مطلوب یا نامطلوب تلقی شوند. البته مطلوب بودن فازی بوده و میتوان برخی از ارزشها را کاملاً مطلوب، تقریباً مطلوب، کمی نامطلوب و …. در نظر گرفت.
مفهوم رابطه علّی
اثر تغییر2 حالت یک شی بر تغییر حالت یک شی دیگر، رابطه علی نامیده میشود. رابطه علّی 3بین دو شی را به دو صورت میتوان بیان کرد:
رابطه بین مقدار حالتهای دو شی
رابطه بین ارزش حالتهای دو شی
این دو نوع رابطه، هم ارز هستند. هم ارزی این دو رابطه، گزاره اساسی الگوی علّی نامیده میشود.
رابطه علّی را با 4 رویکرد مفهومی میتوان بیان کرد. این رویکردها عبارتند از:
رویکردهای مبتنی بر رابطه بین مقدار حالت ها
وقوع حالتی از یک شی (معلول) به وقوع حالتی از شی دیگر (علت) وابسته است.
یک شی (علت) به شی دیگر (معلول) نیرو وارد میکند.
تغییر حالت یک شی (علت) انرژی تولید میکند و حالت شی دیگر (معلول) با دریافت تمام یا بخشی از انرژی تولید شده، تغییر میکند.
رویکرد مبتنی بر رابطه بین ارزش حالت ها
ارزش حالتی از یک شی (علت) به ارزش حالتی از شی دیگر (معلول) وابسته است.
مفاهیم «معلول و دلیل» و «علت و مدلول» مصداقهای یکسان دارند و تفاوت آنها در نام، برای نشان دادن تفاوت رویکرد میباشد. این 4 رویکرد مفهومی، بدیل یکدیگر بوده و هر یک برای مشخصسازی یک رابطه کافی هستند؛ البته هر کدام در مواردی ممکن است کاراتر باشند و گاهی لازم است برای مشخصسازی یک الگو از چند رویکرد استفاده کرد.
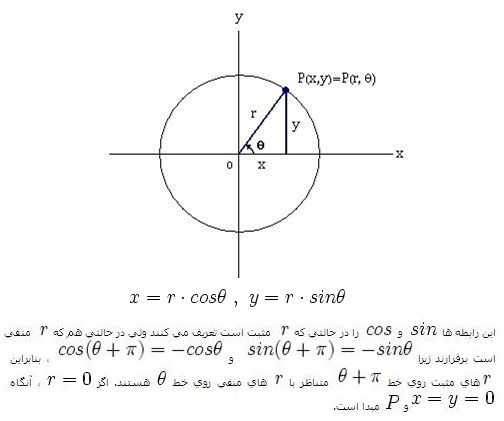
مثال: دستگاههای مختصات دکارتی و قطبی رویکردهای مفهومی بدیل میباشند. هر یک از مختصات دکارتی و قطبی برای مشخصسازی مختصات یک نقطه کافی هستند، اما هرکدام برای کابردی کاراتر میباشند. مختصات یک نقطه در دستگاه دکارتی شامل فاصله از محور افقی و عمودی میباشد. برای هر نقطهی دلخواه چون (p(x,y در مختصات دکارتی، میتوان نمایشی تحت عنوان مختصات قطبی در نظر گرفت. برای این منظور کافی است P را به صورت (p(r,θ نمایش دهیم که در آن طول پاره خط واصل بین مبدا مختصات و نقطه P و θ زاویهی بین پاره خط فوق با جهت مثبت محور X هاست. r را فاصلهی شعاعی و θ را زاویهی قطبی مینامند. وقتی در یک صفحه از هر دو نوع مختصات قطبی و دکارتی استفاده میکنیم، معمولاً مبدا دستگاه قطبی را در مبدا دستگاه دکارتی قرار میدهند و قسمت مثبت محور Xها را به عنوان خط 0=θ در نظر میگیرند. خط θ=π/2 قسمت نامنفی محور y هاست. همان طور که شکل نشان میدهد، این دو مجموعهی مختصات، با معادلههای زیر به هم مربوط میشوند:
رابطه علی و مفاهیم آن (علت، معلول، دلیل، مدلول) مفاهیم انتزاعی هستند که در اصل به اشیاء خارج از ذهن نسبت داده میشوند. البته همان طور که اشیاء غیر ذهنی در فضای ذهنی متناظر دارند، رابطه بین اشیاء غیر ذهنی نیز متناظری در فضای ذهنی دارد. باید دقت کرد که رابطه علی از برخی روابط بین اشیاء غیر ذهنی انتزاع میشود و استفاده از مفاهیم الگوی علّی برای مفاهیم ذهنی در واقع نگاشت روابط غیر ذهنی در فضای ذهنی است.
مثال: نقدینگی و تورم دو مفهوم ذهنی انتزاعی هستند که در جهان خارج از ذهن وجود ندارد. رابطه بین مصادیق این دو مفهوم در جهان خارج از ذهن رابطه علی است و از طریق این مصادیق رابطه علی بین دو مفهوم نقدینگی و تورم ایجاد میشود.
مثال: با فشردن پدال گاز خودرو سوخت بیشتری وارد موتور شده، حرکت موتور افزایش یافته و جابه جایی خودرو افزایش مییابد. با افزایش مسافت طی شده در یک دوره زمانی، سرعت (بنا به تعریف 4) افزایش مییابد. سرعت (یک مفهوم ذهنی) معلول فشرده شدن پدال گاز (یک شی غیر ذهنی) است.
روابط بین اشیاء ذهنی که از تعریف مفاهیم ایجاد میشود روابط علی نیستند. این روابط نباید با رابطه علی ناشی از تناظر رابطه علی بین اشیاء غیر ذهنی اشتباه شوند.
مثال: سود برابر است با کسر هزینه از درآمد. تغییر هزینه و درآمد بر میزان سود اثر میگذارند اما رابطه بین هزینه و درآمد با سود رابطه علی نیست. روابط بین مقادیر متغیرها نیز همیشه رابطه علی نیست.
مثال: رابطه همبستگی بین فراوانی حالتهای مصادیق دو شی عام برقرار بوده و نشان دهنده رفتار گذشته آن دو شی میباشد. اگر بین دو شی رابطه علّی برقرار باشد، آن دو شی همبستگی بالایی با یکدیگر دارند، اما اگر رابطه همبستگی بین دو شی برقرار باشد، نمیتوان نتیجه گرفت که بین آن دو شی رابطه علّی برقرار است.
مفاهیم مربوط به مقدار حالت ها
مفاهیم علت و معلول
معلول 5: شیای که وقوع حالت آن به وقوع یک یا چند حالت شی دیگری بستگی دارد، نسبت به آن شی نقش معلول را دارد. واژه اثر نیز به مفهوم معلول اشاره دارد. عبارت «الف بر ب اثر دارد.» معادل «الف حالت ب را تغییر میدهد.» یا «الف علت ب است.» یا «ب معلول الف است» میباشد.
علت 6: شیای که وقوع حالتی از آن بر وقوع حالت شی دیگری اثر دارد، نسبت به آن شی، نقش علت را دارد. واژه عامل 7(کارگزار) نیز به مفهوم علت اشاره دارد.
در مورد مفاهیم فوق به نکات زیر باید توجه کرد 8:
نقشهای علت و معلول محدود به همان رابطهای است که آن نقش را ایجاد کرده است. مثلا ممکن است یک شی نسبت به شیای علت و نسبت به شی دیگری معلول باشد.
اگر مصداقی از یک شی عام نقش علت یا معلول داشته باشد، شی عام نیز همان نقش را دارا میباشد.
اگر یک جزء از یک شی کل، نقش علت یا معلول داشته باشد، شی کل نیز همان نقش را دارا میباشد.
مفهوم رابطه علّی با تفکیک انواع علتها مشخصتر میشود. در ماتریس زیر انواع علتها آمده است:
| تعریف | |
| کافی (تام) | مجموعهای از علتها که با وقوع آنها، معلول واقع میشود. (این مجموعه ممکن است تنها یک عضو داشته باشد.) |
| ناکافی (ناقص) | مجموعهای از علتها که با وقوع آنها، معلول واقع نمیشود. |
| لازم (انحصاری) | علتی که اگر در مجموعهای از علتهای یک معلول نباشد، معلول با آن مجموعه علتها واقع نمیشود. به عبارت دیگر علت دیگری نمیتواند نقش علت لازم را دریک مجموعه علت داشته باشد. |
| غیر لازم (جانشین پذیر) | علتی که لازم نباشد. به عبارت دیگر علتی که علت دیگری میتواند نقش آن را دریک مجموعه علت داشته باشد. |
| مانعه الجمع | چند علت که میتوانند جانشین یکدیگر شوند اما اگر با هم باشند اثر یکدیگر را خنثی میکنند. |
| بازدارنده (مانع) | علتی که اگر در مجموعهای از علتهای یک معلول باشد، معلول با آن مجموعه علتها واقع نمیشود. |
| پیش برنده (غیر مانع) | علتی که مانع نباشد. |
| نگهدارنده (حقیقی) | علتی که با هر تغییر جهت آن، معلول تغییر میکند. |
| محرک (معد) | علتی که تنها تغییر در یک جهت آن، معلول را تغییر میدهد. |
| بی واسطه (مستقیم) | اگر بین یک علت با معلولش، علت دیگری نباشد، آن علت، بی واسطه نامیده میشود. |
| با واسطه(غیر مستقیم) | اگر بین یک علت با معلولش، علت دیگری باشد، آن علت، با واسطه نامیده میشود. |
| مداخله کننده | علتی که بر رابطه بین یک علت و معلول اثر میگذارد. در واقع، علت مداخله کننده بر یک شی در مسیر علت و معلولی که بی واسطه در نظر گرفته شدهاند اثر میگذارد اما چون آن شی آورده نشده، تلویحاً گفته میشود که بر رابطه اثر میگذارد. |
| بالفعل | علتی که در یک زمان معین بر معلول اثر میگذارد. |
| بالقوه (پتانسیل) | علتی که بالفعل نیست. |
| بنیادی | نهادی و اساسی است |
| جانبی |
در مورد انواع علتها به نکات زیر باید توجه کرد:
ممکن است نقش یک مجموعه علتها با نقش یک عضو آن متفاوت باشد. بی واسطه یا با واسطه بودن بستگی به میزان تفصیل یا تقلیل شبکه دارد. ممکن است علتی در یک شبکه با واسطه باشد و در زیر شبکهای از آن شبکه، نقش بی واسطه را داشته باشد.
علتهای غیرلازم، غیر مانع و بالقوه بر معلول اثر دارند. چون علت است. غیرلازم بودن،غیر مانع بودن و بالقوه بودن به معنای غیر موثر بودن نیست.
علت مانع و غیر مانع ویژگی فازی دارد.
اگر علتی بالفعل باشد، ارزش حالتهای آن لزوماً با ارزش حالتهای معلول یکسان است.
اگر علت الف برای معلول ب بالقوه و برای معلول ج بالفعل باشد، ارزش حالتهای الف با ارزش حالتهای ج یکسان بوده و لزوماً با ارزش حالتهای ب یکسان نیست.
یک علت ممکن است چندین نقش داشته باشد. (یک شی در رابطه با معلولها مختلف، نقشهای متفاوت داشته باشد.)
ممکن است نقش یک علت برای یک معلول در ترکیب با مجموعه علتهای متفاوت، متفاوت باشد.
مثال: یک مجموعه از علتها برای معلولی کافی باشند اما یکی از آن علتها به تنهایی کافی نباشد.
مثال: الف علت لازم ب و علت غیرلازم ج و معلول د باشد.
مثال: یک شی در یک مجموعه لازم بوده و در مجموعه دیگری نالازم باشد.
در ماتریس زیر ترکیب نقشهای علی نمایش داده شده است.
| نگهدارنده | معد | |||||||||
| غایی | کافی | لازم | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| نالازم | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| ناکافی | لازم | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| نالازم | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | ||
| کافی | لازم | |||||||||
| نالازم | ||||||||||
| ناکافی | لازم | |||||||||
| نالازم | ||||||||||
مثال: برخی از علتهای یک ساختمان در ماتریس زیر آمده است. علتی که در ستون مصداق ذکر شده، تمامی نقشهای ذکر شده در ستون نقشها را نسبت به ساختمان دارد.
مفاهیم انرژی، نیرو و کار
انرژی 9: در تغییر حالت یک شی انرژی تولید و یا مصرف میشود.
انواع انرژی:
پتانسیل (بالقوه)
جنبشی
نیرو10: برای تغییر حالت یک شی به آن نیرو وارد میشود.
انواع نیرو:
نیروهای بنیادی
نیروی اصطکاک
کار11: حاصل ضرب نیرو (نیرویی که علت به معلول وارد میکند) در مقدار تغییر حالت معلول،کار نامیده میشود.
واژههای کار و انرژی مفهوم یکسان دارند (مشترک معنوی هستند.)، اما دلالتهای آنها متفاوت است 12. کار انجام شده بر روی یک جسم، به صورت انرژی در آن ذخیره میشود و آزاد شدن انرژی، کار انجام میدهد. بنابراین یکای13 کار و انرژی یکسان است 14.
مثال: اگر با اعمال نیروی f جسمی به جرم m را از روی زمین بلند کرده و در ارتفاع h از زمین قرار دهیم، در این صورت بر روی این جسم مقداری کار انجام دادهایم. این کار به صورت انرژی پتانسیل در جسم ذخیره میشود. یعنی جسم در ارتفاع h که در حالت سکون قرار دارد، دارای انرژی mgh میباشد.(f=mg) اگراین جسم را از ارتفاع h رها کنیم، این انرژی آزاد میشود. بنابراین کار میتواند به انرژی تبدیل شود.
توان15: مقدار کار در واحد زمان توان نامیده میشود. به عبارت دیگر آهنگ16 (نرخ) کار توان نامیده میشود. آهنگ مصرف انرژی نیز توان نامیده میشود.
اگر مقدار نیرو و تغییر حالت معلول قابل اندازهگیری باشند، مقدار انرژی، کار و توان قابل اندازهگیری میباشد.
کار را میتوان با معیار ارجاع به علت، با دو دلالت بیان کرد:
عمل17: کار با ارجاع به علت تغییر، عمل نامیده میشود. به عبارت دیگر اگر عامل معلوم باشد، کار «عمل» نامیده میشود.
رویداد18(واقعه): کار بدون ارجاع به علت تغییر، رویداد نامیده میشود. به عبارت دیگر اگر عامل مجهول باشد، کار «رویداد» نامیده میشود.
سایر مفاهیم مرتبط:
عامل19(کارگزار): علت نسبت به عمل، عامل نامیده میشود.
فرایند20: سامانهای از چند کار است. در فرایند، حداقل یکی از خروجی یک کار، ورودی کار دیگر است. به عبارت دیگر فرایند کاری است که شامل چند زیر کار متوالی است.
رفتار21: توالی زمانی حالتها یک شی رفتار نامیده میشود.
مفهوم منبع و هزینه
منبع22: شیای که میتواند نقش یک علت را داشته باشد، نسبت به معلول آن علت، نقش منبع را دارد. به عبارت دیگر منبع، علت بالقوه است و اگر بالفعل شود نقش علت (برای معلول) را خواهد داشت و دیگر نقش منبع ندارد.
هزینه: مقدار منابع استفاده شده هزینه نامیده میشود. مقدار پول معادل با مقدار استفاده از منبع، هزینه پولی نامیده میشود.
اسراف23 (اتلاف): استفاده نادرست از منبع، اسراف نامیده میشود.
استفاده نادرست شامل موارد زیر میشود:
استفاده بیش از حد از منابع سرمایه ای
بدون استفاده ماندن یک منبع
استفاده در نقشی که اولویت ندارد.
مثال: پول هنگامی نقش منبع را دارد که برای انجام کاری در نظر گرفته شود. در چنین مواردی میتوان از مفهومهای تخصیص یا توزیع منبع برای پول استفاده کرد. اما در مواری که پول بین وراث تقسیم میشود، دیگر توزیع منبع نیست، توزیع سهم است. جالب است که در بسیاری از فرایندهای برنامهریزی، تقسیم بودجه توزیع منابع نیست بلکه تقسیم سهم است!
| تعریف | مثال | |
| مصرفی (مواد اولیه) | منبعی که جزیی از معلول میشود. منبع مصرفی متناظر با علت داخلی است. | |
| سرمایهای (ابزار) | منبعی که جزیی از معلول نمیشود. البته منبع سرمایهای به تدریج مستهلک میشود. منبع مصرفی متناظر با علت خارجی است. |
مفاهیم مربوط به ارزش حالت ها
مفاهیم دلیل و مدلول
اگر به رابطه علی به صورت رابطه بین ارزش حالتهای علت و معلول توجه شود، معلول نقش دلیل و علت نقش مدلول را خواهد داشت.
تعریف مفاهیم دلیل و مدلول به شرح زیر میباشد:
دلیل24: شیای که ارزش حالتهای آن بر ارزش حالتهای شی دیگری اثر میگذارد، نسبت به آن شی، نقش دلیل را دارد.
مدلول: شیای که ارزش حالتهای آن به ارزش حالتهای شی دیگری بستگی دارد، نسبت به آن شی نقش مدلول را دارد.
دلیل برای شیای که دارای اختیار باشد میتواند نقش علت داشته باشد. به عبارت دیگر هنگامی که شخص دارای اختیار با هدف رسیدن به نتیجهای، اقدامی را انجام میدهد؛ آن نتیجه (حالت) دلیلی است که علت اقدام شده. البته باید توجه داشت که دلیل نسبت به مدلول نقش معلول دارد و نقش علت آن نسبت به شی سوم (شخص دارای اختیار) میباشد. دلیل در نقش علت، علت غایی نامیده میشود. برای دلیل (به عنوان یک علت) میتوان انواع نقشهای کافی، ناکافی، لازم، نا لازم و … را در نظر گرفت.
مفاهیم معیار و خطمشی
مفاهیم معیار و خطمشی به ارزش حالتهای دلیل و مدلول مربوط میشود. تعریف این دو مفهوم عبارتند از:
ارزش حالتهای دلیل، معیار نامیده میشود.
ارزش حالتهای مدلول، «خطمشی25 (سیاست)» نامیده میشود.
به عبارت دیگر، ارزش حالتهای یک شی، نقش معیار برای اشیایی که علتهای آن شی هستند دارند. همچنین ارزش حالتهای علتها، خطمشیهای هستند که از معلول استنتاج میشوند.
مثال: ایمنی یک خطمشی عمومی است که در انتخاب وسیله نقلیه برای سفر باید رعایت شود. معیار این خطمشی، سلامتی میباشد.
خطمشیهای مربوط به یک موضوع با توجه به مرز موضوع به سه دسته تقسیم میشوند:
خطمشیهای درونی: خطمشیهای مربوط به اشیاء درون موضوع که معیار آنها نیز درون موضوع باشند، خطمشی درونی مینامیم. به عبارت دیگر علت و معلول درون موضوع قرار دارند.
خطمشیهای ورودی: خطمشیهایی که مربوط به اشیاء درون موضوع بوده و معیار آنها بیرون از موضوع باشند، خطمشیهای ورودی (وارد شده از محیط) مینامیم. به عبارت دیگر معلول خارج از موضوع بوده و علت درون موضوع است.
خطمشیهای خروجی: خطمشیهایی که مربوط به اشیاء بیرون از موضوع بوده و معیار آنها درون موضوع باشند، خطمشیهای خروجی (وارد شده به محیط) مینامیم. به عبارت دیگر معلول درون موضوع بوده و علت خارج از موضوع است.
معمولاً مصادیق خطمشی و راهبرد با یکدیگر اشتباه گرفته میشود. تفاوتهای بین این دو مفهوم عبارتند از:
راهبرد از جنس مقدار حالت است و خطمشی از جنس ارزش حالت. راهبرد خود یک هدف است که در رابطه با هدفی دیگر، نقش راهبرد پیدا میکند؛ خطمشی ارزشهای مدلول نسبت به ارزشهای دلیل است. راهبرد حالتی است که باید حاصل شود و خطمشی، ارزشی است که باید رعایت شود.
هنگامی که یک خطمشی در طراحی اعمال میگردد، کارکرد مشخصسازی آن به هدف انتخاب شده منتقل شده و ذکر آن خطمشی تنها به عنوان مستندات تصمیم در گزارش طراحی آورده میشود.
مفهوم سامانه علّی
تعریف سامانه علی
سامانه علی26شامل چند شی27 به همراه روابط علی بین آنها میباشد. سامانه علّی آن قدر گسترده است که کل جهان را در بر میگیرد28. بنابراین هر سامانه علّی محدود، زیرسامانهای از سامانه علّی جهانی است.
روابط بین اشیاء در یک سامانه علی
یک شی در سامانه علی ممکن است برای چند شی نقش علت و برای چند شی دیگر نقش معلول را داشته باشد.
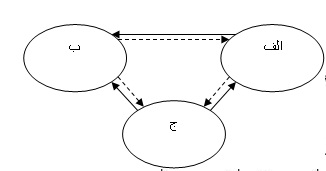
مثال: ارتباط بین سه حوزه در شکل زیر نمایش داده شده است. کمانهای پیوسته نماد رابطههای مقداری و کمانهای خط چین نماد رابطههای ارزشی هستند. خطمشی حوزه الف از حوزه ب حاصل میشود. حوزه الف معیار حوزه ج میباشد. حوزه ب معیار الف و ج میباشد و خطمشیهای آن به الف و ج بستگی ندارد. خطمشیهای ج از الف و ب حاصل میشود اما معیار الف و ب نیست.
با حوزهبندی یک سامانه و یافتن روابط بین حوزهها میتوان خطمشیهای ناظر بر یک حوزه مورد نظر را محاسبه کرد. اگر یک شی چند معلول داشته باشد، (تابع ارزش آن بستگی به تابع ارزش همه معلول داشته و) چندین معیار خواهد داشت. ممکن است خطمشیهای حاصل از معیارهای مختلف با یکدیگر در تناقض باشند. در موارد تناقض برای تعیین تابع ارزش مدلول، برخی از معیارها رعایت نمیشوند29. تناقض ممکن است ناشی از خطای محاسبه یا تناقض دو معیار باشد.
مثال: خشک نکردن آب وضو مستحب است و رد احسان نادرست. حال اگر پس از وضو حوله بیاورند، خطمشی خشک نکردن آب وضو را باید رعایت کرد یا رد نکردن احسان را؟ چون اهمیت رد احسان بالاتر است، در چنین موقعیتی باید حوله را گرفت و خطمشی خشک نکردن آب وضو را نباید رعایت کرد!
تراز (حالت سامانه)
حالتهای متناظر اشیاء یک سامانه علی، یک تراز نامیده میشوند. اگر یک سامانه علی را به عنوان یک شی در نظر بگیریم، تراز این سامانه همان حالت کل سامانه (به عنوان یک شی) میباشد.
مشخصات تراز:
ممکن است یکی از حالتهای یک شی در چند لایه عضو باشد.
ممکن است یک تراز شامل چندین حالت بدیل از یک شی باشد.
متناظر با حالتهای واقعی، مطلوب، حقیقی و … ترازهای واقعی، مطلوب، حقیقی و … مطرح هستند.
تعریف انواع ترازها:
تراز واقعی: ترازی که تمام حالتهای عضو آن، حالت واقعی هستند.
تراز مطلوب: ترازی که تمام حالتهای عضو آن، حالت مطلوب هستند.
تراز حقیقی: ترازی که تمام حالتهای عضو آن، حالت حقیقی هستند.
تراز بالقوه: تراز که تمام حالتهای آن بالقوه هستند.
تراز بالفعل: تراز بالفعل ترازی است که در صورت عدم مداخله، حالتهای آن در طول زمان بالفعل میشوند. در یک تراز بالفعل ممکن است برخی از حالتها بالقوه باشند اما در طول زمان با بالفعل شدن علت هایشان بالفعل خواهند شد.
تابع ارزش تراز، رجحان بین ترازها را بیان میکند.
توصیف سامانه علّی
یک سامانه علّی را میتوان با دو رویکرد ساختاری و یا رفتاری توصیف کرد. رویکرد ساختاری، نمایش دهنده اجزاء سامانه و روابط علّی بین آنها میباشد. رویکرد رفتاری، نمایش دهنده اجزاء سامانه و روابط توالی زمانی بین حالتها یک یا چند جزء میباشد30 هر کدام از این دو رویکرد بخشی از اطلاعات مر بوط به یک سامانه را بیان میکنند. گاهی برای توصیف یک سامانه از توصیف هر دو رویکرداستفاده میشود.
رویکرد ساختاری یا رفتاری را با زبان های31 متعددی میتوان بیان نمود32. برخی از زبانها عبارتند از زبان طبیعی (فارسی، عربی و…)، گراف، مکان هندسی، ماتریس، معادله و… دقت و نوع اطلاعات قابل بیان در هر زبان متفاوت است. معمولا از ترکیب چند زبان برای توصیف یک رویکرد استفاده میشود.
توصیف سامانه علّی با زبان طبیعی
با زبانهای طبیعی میتوان تمام مشخصات یک سامانه را بیان نمود. سایر زبانها این کارکرد را نداشته، اما در بیان برخی از مشخصات کارایی بیشتری نسبت به زبانهای طبیعی دارند. بهتر است الگو با زبانهای گراف، مکان هندسی و … ساخته شود و از زبان طبیعی برای ارائه توضیح در مورد الگوی ساخته شده استفاده شود.
برخی از خطمشیهایی که برای افزایش دقت توصیف با زبان طبیعی باید رعایت شوند عبارتند از33:
در قالب جمله شرطی، علت در بخش اگر و معلول در بخش آنگاه آورده شود.
حشو (افزونگی) در جملات کاهش یابد.
واژههای مترادف آورده نشود.
از جملات کوتاه استفاده شود.
از نمادهای نگارش (.،؛ « » () -: ) در متن استفاده شود.
توصیف سامانه علّی با زبان گراف
زبان گراف برای نشان دادن تمایز بین اجزاء و روابط بین آنها کارایی خوبی دارد، اما دقت زیادی ندارد. با استفاده از زبان گراف، مفاهیم (شبکه 34، درخت، مسیر، مدار و … ) و گزارههای نظریه گراف نیز قابل استفاده خواهند بود. در نظریه گراف برای انواع گرهها یک نماد و برای انواع کمانها دو نماد (بدون جهت و جهت دار) در نظر گرفته شده است. اما در گرافهای خاص میتوان برای افزایش ارائه اطلاعات، از نمادهای خاصی (که در نظریه گراف مطرح نیستند) استفاده کرد.
اگر الگوی یک شی با گراف بیان شود، الگوی حاصل گسسته35 و تقلیل یافته36 است 37.
برای افزودن توضیح به گراف ساختار و رفتار میتوان از نمادهای ماتریس زیر استفاده کرد:
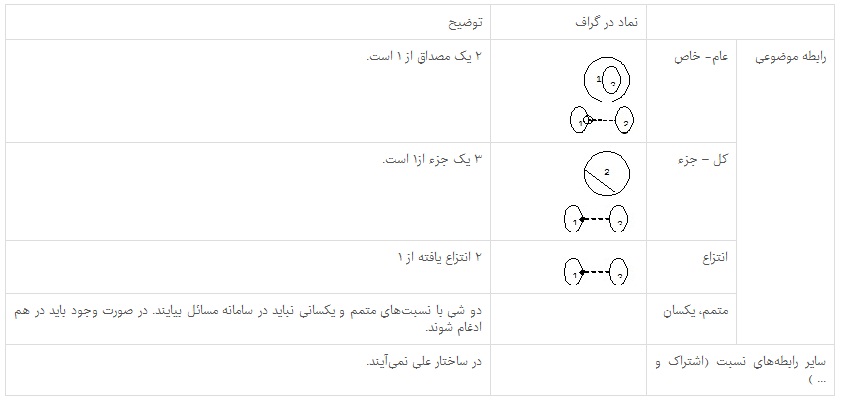
برای افزودن رابطههای مفهومی به گراف ساختار و رفتار میتوان از نمادهای ماتریس زیر استفاده کرد:
توصیف ساختار با زبان گراف
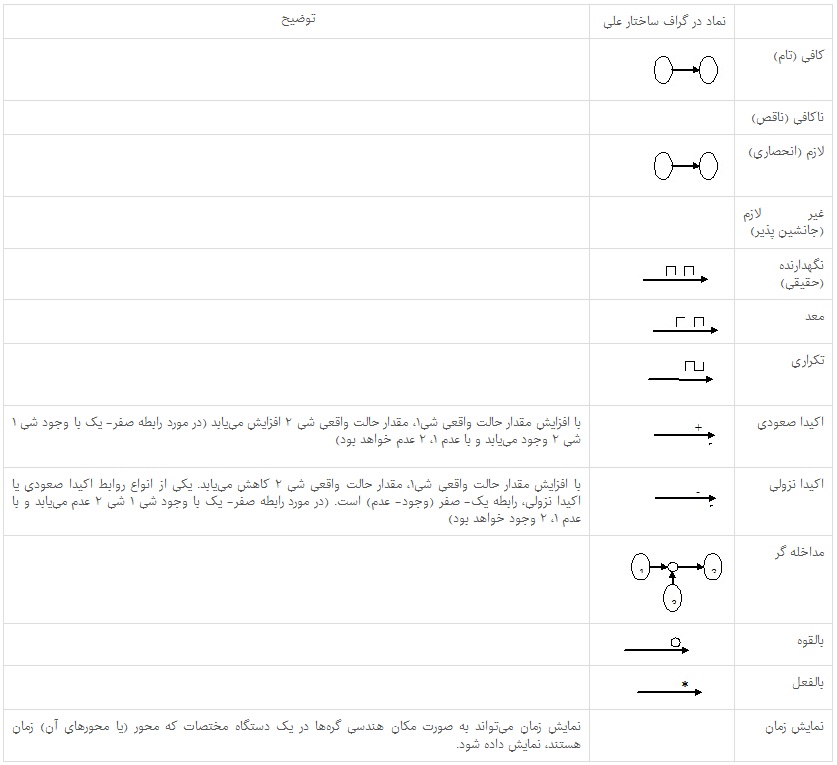
نمادهای گراف ساختار علی در ماتریس زیرآمده است:
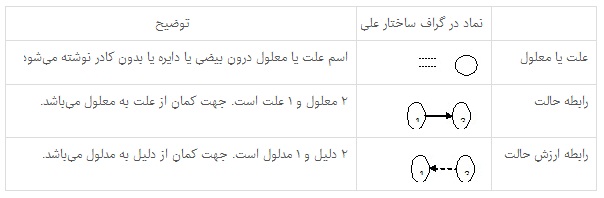
در مواردی که دلیل بر معلول واقعی منطبق نباشد، رابطه حالت و ارزش حالت بریکدیگر منطبق نخواهند شد. این عدم تطابق هنگامی پیش میآید که پیشبینی تصمیمگیرنده مطابق واقعیت نباشد. برای افزایش مشخصات رابطه علّی در گراف ساختار، میتوان از نمادهای ماتریس زیر استفاده کرد:
نمادهای بالا، یک رابطه علّی را با دقت بالایی نمایش نمیدهند، اما همین مقدار دقت مفید است.
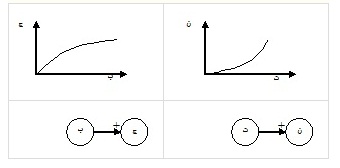
مثال: دو رابطه علّی که در نمودارهای زیر با زبان مکان هندسی بیان شده را در نظر بگیرید. چون هر دو تابع، اکیدا صعودی هستند برای هر دو از نماد + در گراف ساختار استفاده میشود، هرچند شکل این دو منحنی خیلی تفاوت دارد.
توصیف رفتار با زبان گراف
دو روش برای نمایش حالتها و روابط بین آنها به صورت گراف وجود دارد:
نمایش حالتها با گره و رابطه بین حالتها با کمان: در این صورت، «گراف رفتار» نمودار حالت یا نمودار گذر حالت38 نامیده میشود39.
نمایش حالتها با کمان و رابطه بین حالتها با گره: در این صورت «گراف رفتار» نمودار فرایند نامیده میشود.
این دو صورت دوگان یکدیگر هستند40.
مثال: دو گراف زیر دوگان هستند. اجزاء متناظر با خط چین نمایش داده شده است.
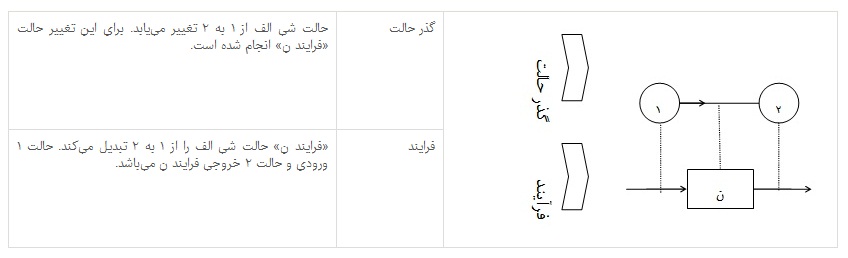
با کاری که علت انجام میدهد، حالت شی را تغییر میکند. حالت قبل از فرایند، ورودی و حالت بعد از فرایند، خروجی نامیده میشود. با توجه به این که در گراف رفتار، حالتهای یک شی با چند گره یا کمان نمایش داده میشود باید دقت کرد که هر گره یا کمان نماینده یک شی نیست بلکه هر گره یا کمان یک حالت از یک شی را نمایش میدهد. البته گراف رفتار ممکن است شامل چند شی باشد، به عبارت دیگر همه گرهها و کمانها مربوط به یک شی نباشند.
توصیف رفتار با زبان گراف به صورت نمودار گذر حالت
در گراف گذر حالت، حالتها با گره و رابطه بین حالتها با کمان نمایش داده میشود. نمادهای گراف رفتار به صورت نمودار گذر حالت در ماتریس زیرآمده است.

توصیف رفتار با زبان گراف به صورت نمودار فرایند
در گراف فرایند، حالتها با کمان و رابطه بین حالتها با گره نمایش داده میشود. رابطه بین حالتها متناظر با فعالیتی است که حالت را تغییر میدهد. بنابراین با رویکردی دیگر میتوان نمودار فرایند را توصیف فعالیتها و رابطه آنها (که حالتها هستند) در نظر گرفت.
نمادهای گراف رفتار به صورت نمودار فرایند در ماتریس زیرآمده است.
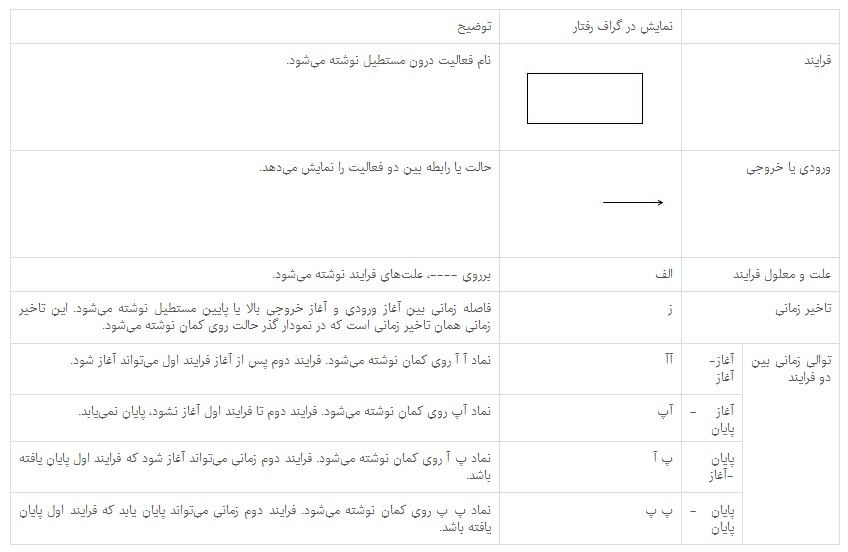
فاصله زمانی بین فرایند بعد از نمادهای توالی نوشته میشود.
مثال: در زیر رفتار نمایشگر یک دستگاه خودپرداز با نمودار فرایند توصیف شده است. این گراف یک شیای است.
ترکیب گرافهای ساختار و رفتار
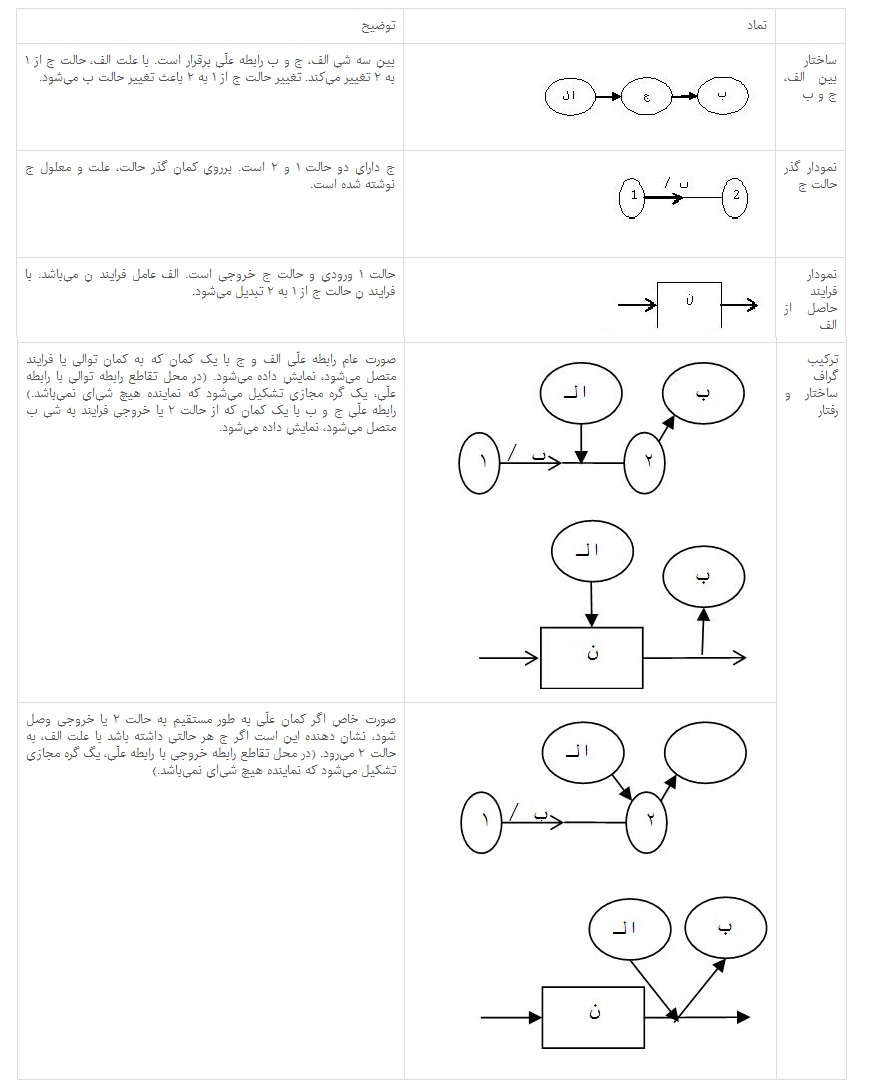
گراف ساختار، رابطههای علّی بین حالتهای اجزاء و گراف رفتار، رابطههای توالی زمانی بین حالتهای کل یا اجزاء یک شی را نمایش میدهد. در ماتریس زیر نحوه ارتباط گراف ساختار و رفتار نمایش داده شده است.
توصیف سامانه علّی با زبان مکان هندسی
توصیف ساختار با زبان مکان هندسی
برای نمایش مکان هندسی41 رابطه بین معلول و علتهای آن، یکی از محورهای دستگاه مختصات (مثلاً Y ) به مقادیر معلول و سایر محورها به علتها (برای هر کدام از علتها یک محور) تخصیص مییابد. مجموعه نقاط تلاقی مقادیر متناظر معلول و علتها، مکان هندسی رابطه علّی را نمایش میدهند. بعد دستگاه مختصات برای نمایش مکان هندسی برابر است با تعداد علتها به اضافه یک. اگر معلول تنها یک علت داشته باشد، دستگاه مختصات 2 بعدی بوده و مکان هندسی در صفحه قرار میگیرد.
مثال: در زیر، ساختار رابطه علّی الف و ب با مکان هندسی، گراف و ماتریس تراز نمایش داده شده است. در ماتریس تراز، مقادیر حالتهای ب در ستون اول مقادیر حالتهای الف در ستون دوم آمده و هر ردیف شامل مقادیر متناظر میباشد. یکی از روابط علّی بین الف و ب چنین است: اگر مقدار حالت ب، 4 باشد، مقدار حالت الف، 3 خواهد بود.
اگر هر رابطه علّی را با یک مکان هندسی نمایش دهیم، توصیف سامانه علّی شامل مکانهای هندسی دو بعدی به تعداد رابطههای علّی خواهد بود. اگر برخی از مکانهای هندسی شامل بیش از یک علت باشند، (بعد آن بیش از 2 بوده) و به تعداد بعدهای اضافه، از تعداد مکانهای هندسی 2 بعدی کاسته خواهد شد.
توصیف رفتار با زبان مکان هندسی
مکان هندسی رفتار در یک دستگاه مختصات 2 بعدی رسم میشود که محور افقی (X) آن زمان و محور عمودی آن (Y) حالتهای شی میباشد. مکان هندسی رفتار گاهی نمودار زمانبندی نامیده میشود.
مثال: در نمودارهای زیر مکان هندسی رفتار شاخصهای بورس اوراق بهادار تهران از تاریخ 83/1/1 تا 84/1/1 نمایش داده شده است.
مثال: در زیر، گراف ساختار (سمت چپ) و مکان هندسی رفتار (سمت راست) اشیاء یک سامانه علّی نمایش داده شده است. اجزاء سامانه توصیف شده دوحالته هستند. (یا مقادیر حالت آنها در دوطبقه دستهبندی شدهاند.) در این سامانه، الف علت کافی و معد برای ب و علت کافی و نگهدارنده برای ج میباشد. هنگامی که حالت الف، به مقدار اول باز میگردد، ج نیز به حالت اول خود باز میگردد. ج علت د است و بین وقوع علت و معلول، تأخیر زمانی 1ز – ز3 وجود دارد. ب و د، با هم علتهای کافی برای ه هستند.
مثال: برای توصیف رفتار هر متغیر یک مکان هندسی لازم است. اگر برای توصیف یک شی از چند متغیر (که جزء آن یا انتزاع از آن باشند) استفاده شود، برای توصیف هر کدام یک مکان هندسی لازم است.
علاوه بر رفتار، حالت یک شی در یک مقطع زمانی را نیز میتوان با مکان هندسی نمایش داد. مکان هندسیهایی که حالت را نمایش میدهند دارای بعد زمان نیستند. نمایش حالت بک شی عام با مصادیق مقطعی: توزیع فراوانی مصدیق، حالت شی بوده و مکان هندسی توزِِیع فراوانیها، مکان هندسی یک حالت میباشد. توزیع فراوانی با انواع نمودارها (میلهای، منحنی، مساحتی و…) قابل نمایش است. برای هرکدام از مشخصههای توزیع فراوانی (میانگین، واریانس و…)، میتوان یک مکان هندسی رفتار ترسیم کرد، که تغییر آنها را در طول زمان نماش میدهد.
نمایش حالت های(تراز) یک شی با چند متغیر: در صورتی که حالت یک شی با چند متغیر توصیف شود، میتوان از انواع نمودارها (میلهای، منحنی، مختصاتی، راداری و …) برای نمایش تراز آن شی استفاده کرد.
توصیف سامانه علّی با زبان ماتریس
توصیف ساختار با زبان ماتریس
ساختار یک سامانه علی با یک ماتریس42 مربعی داده میشود که سطرها و ستونهای ماتریس احزاء سامانه بوده و آرایههای ماتریس، نشان دهنده ارتباط بین اجزاء میباشد. چنین ماتریسی ماتریس —- گراف سامانه میباشد.
توصیف رفتار با زبان ماتریس
رفتار یک سامانه علی با یک ماتریس نمایش داده میشود که ستونها (با سطرها) آن نماینده متغیر زمان و سطرها (یا ستونها) نماینده اجزاء سامانه هستند. آرایههای ماتریس مقادیر حالتهای هر جزء در زمانهای مشخص شده در ستونهای (یا سطرهای) ماتریس هستند.
ماتریس رفتار لزوماً تناظر بین حالتهای علت و معلول را نمایش نمیدهد بلکه حالت هر جزء را در مقاطع زمانی معین نمایش میدهد. در مواردی که حالت معلول نسبت به حالت علت تاخیر زمانی دارد، حالتهای متناظر علت و معلول در یک مقطع زمانی رخ نمیدهد.
تناظر بین حالتهای یک سامانه علی را میتوان با ماتریس تراز نمایش داد. در ماتریس تراز هر ستون(یا سطر) نماینده یک جزء از سامانه است و هر سطر (یا ستون) حالتهای متناظر اجزاء را نمایش میدهد که نماینده یک تراز است.
توصیف سامانه علّی با زبان معادله
توصیف یک سامانه علّی معادلههای ریاضی و آماری 43 محاسبات را تسهیل میکند.
توصیف ساختار با زبان معادله
رابطه علّی مشخصات تابع را دارد. بنابراین معادله رابطه علّی، معادله یک تابع است که در آن معلول متغیر وابسته و علتها متغیر مستقل هستند. اگر معلول بیش از یک علت داشته باشد تابع علّی چند متغیره خواهد بود. تابع جزیی (که رابطه معلول را تنها با یک علت مشخص میکند) از مشتق جزیی تابع چند متغیره، بدست میآید. با استفاده از سری تیلور میتوان معادله هر مکان هندسی را بدست آورد.
توصیف رفتار با زبان معادله
معادله رفتار یک متغیر طولی، سری زمانی44 نیز نامیده میشود.
گزارههای الگوی علی
یکسانی ارزش حالتهای متناظر علت و معلول (گزاره اساسی الگوی علّی)
گزاره: «ارزش حالتهایی از علت و معلول که با یکدیگر متناظر هستند، یکسان است.»
اثبات: حالت معلول بستگی به حالت علت دارد، اگر بخواهیم معلول، حالت خاصی داشته باشد، علت باید حالت متناظر با آن حالت خاص را داشته باشد.
اگر علتی بالفعل باشد، ارزش حالتهای آن لزوماً با ارزش حالتهای معلول یکسان است. اگر علت الف برای معلول ب بالقوه و برای معلول ج بالفعل باشد، ارزش حالتهای الف با ارزش حالتهای ج یکسان بوده و لزوماً با ارزش حالتهای ب یکسان نیست.
در مثال زیر تناظر بین مجموعههای ارزش حالتهای معلول، مقدار حالتهای معلول، مقدارحالتهای علت و ارزش حالتهای علت نمایش داده شده است.
مثال:
در مثال زیر تناظر بین مکان هندسی تابع ارزش معلول، تابع تناظر حالت و تابع ارزش علت نمایش داده شده است.
مثال:
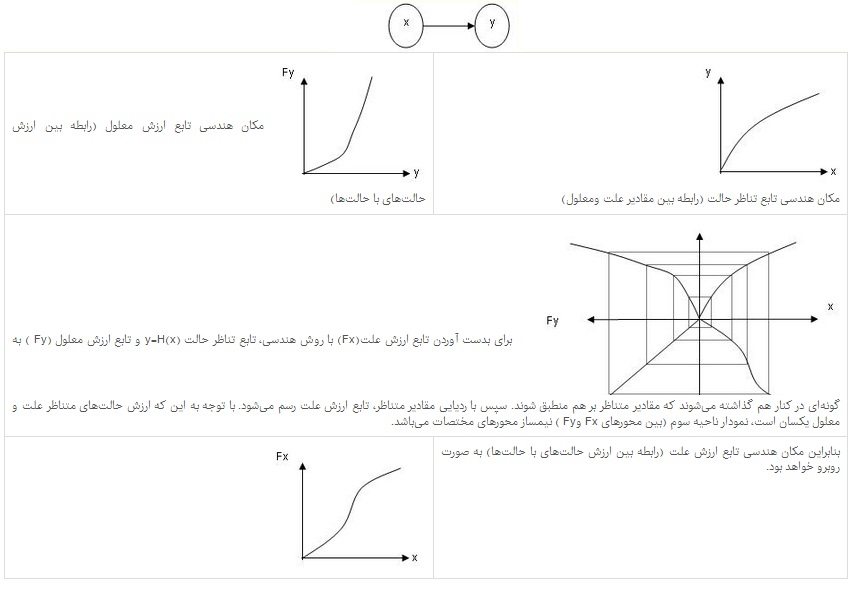
همچنانکه در مثال بالا دیده میشود، تابع ارزش علت، علاوه بر تابع ارزش معلول به تابع تناظر علت و معلول نیز بستگی دارد45.
رابطه ارزشی (رابطه بین ارزش حالتهای علت و معلول) دوگان رابطه مقداری (رابطه بین مقدار حالتهای علت و معلول) است.
اگر ترجیحات شخصی که ارزش حالتهای معلول و علت را تعیین میکند، سازگار باشد، ارزشهای یکسانی برای حالتهای متناظر علت و معلول در نظر میگیرد. به عبارت دیگر، اگر یک شخص بخواهد ترجیحاتش سازگار باشد، باید ارزشهای یکسانی برای حالتهای متناظر علت و معلول در نظر بگیرد.
بودن رابطه علّی
گزاره: «حالتهای معلول، تابع حالتهای علت هستند.» به عبارت دیگر «ارزش حالتهای علت تابع ارزش معلول هستند.»
اثبات: بنا به تعریف یک حالت در نقش علت با ثابت ماندن سایر علتها نمیتواند متناظر با دو حالت از معلول باشد. این تابع را تابع تناظر حالت مینامیم.
ترایایی رابطه علّی
گزاره: «رابطه علی خاصیت ترایایی46 دارد.»
اگر الف علت ب و ب علت ج باشد، الف علت ج خواهد بود. البته اگر ب عام یا کل باشد، در صورتی رابطه ترایایی برقرار است که همان مصادیق یا اجزاء ب که معلول الف هستند، علت ج هم باشند.
دور
گزاره: «دور محال است.» دور یعنی: یک علت، معلول و معلول خودش باشد. یا یک خطمشی، معیار خودش باشد.
اگر هرشی عام که مصادیق 47 آن چند بار، به وجود میآید، از بین میرود یا تغییر میکند هر بار به عنوان یک شی در نظر گرفته شود، ابهام دور از بین خواهد رفت. هر بارکه شیای عام به وجود میآید، از بین میرود یا تغییر میکند، نقش یک علت یا معلول متفاوت را خواهد داشت.
به عبارت دیگر اگر یک ساختار سامانه علی را با زبان گراف نمایش دهیم و هر شی خاص با یک گره نمایش داده شود، گراف حاصل، مسیر بسته و طوقه نخواهد داشت. در صورت وجود اشیاء عام، گراف ممکن است مدار48 (مسیر بسته) یا طوقه داشته باشد اما پدیدآمدن مدار وطوقه نشانه دور نیست.
مثال: چرخه معیوب فقر49
تسلسل
ثابت بودن ارزش
گزاره: «تابع ارزش یک شی خاص ثابت است.»
تابع ارزش هر شیء بستگی به تابع ارزش معلول هایش داشته و در سامانه علی جهانی، معیارهای مطلقی وجود دارند که ارزش تمام اشیاء مبتنی بر آنها هستند.
ابهام نسبی یا ثابت (مطلق) بودن ارزش همان ابهام دور میباشد. اگر یادمان باشد که یک شی عام، نماینده مجموعهای از اشیاء است، تفاوت تابع ارزش هر مصداق به حساب تغییرپذیری ارزش شی عام گذاشته نمیشود.
تابع ارزش یک شی عام ممکن است نسبی باشد. اگر یک شی عام را در نظر بگیریم، با تغییر معلولها یا تغییر تابع ارزش معلولها، تابع ارزش شیء مورد نظر نیز تغییر میکند.
مثال: مطالعه یک کتاب برای امیر خوب است و برای حسن بد است. همین کتاب برای امیر قبلا بد بوده و الان خوب است. مطالعه کتاب مورد نظر یک شی عام بوده و ارزش آن نسبی است اما مطالعه آن کتاب توسط امیر در یک دوره زمانی و مطالعه آن توسط حسن دو شی هستند که ارزشهای متفاوت دارند.
تناظر بین الگو و شئ اصیل
تناظر یک یا چند الگو با چند یا یک شی اصیل
تناظر چند الگو با یک شی اصیل
چند الگو که یک شی (یا یک حوزه از یک شی) را توصیف میکنند، «هم موضوع» نامیده میشوند.
حوزههایی از چند الگو که متناظر با حوزهای از شی اصیل هستند، بایکدیگر متناظر هستند. (رابطه ترایایی در تناظر) البته ممکن است حوزهای در یک الگو باشد که در الگوی دیگر وجود نداشته و بنابراین و متناظری برای آن نباشد.
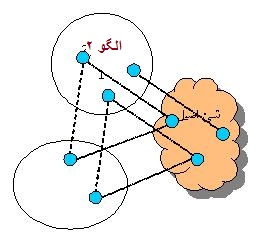
در نمودار زیر تناظر بین الگوها با خط چین و تناظر بین الگوها و شی اصیل با نقطه چین نمایش داده شده است. الگوی 1 شامل حوزهای میشود که متناظری در الگوی 2 ندارد.
حوزههای متناظر بین الگوها ممکن است یکسان یا متفاوت باشند. موارد تفاوت در ماتریس زیر توضیح داده شده است.
| موارد تفاوت | توضیح | |
| میزان جزییات | حوزهای در یک الگو با تفصیل بیشتر نسبت به الگوی دیگر نمایش داده شده باشد. | |
| بعد ساختاری و رفتاری | بعد توصیف برای یکی ساختار و برای دیگری رفتار (به صورت گذرحالت یا فرایند) باشد. | |
| زبان | الگوها با زبانهای مختلف (گراف، مکان هندسی و ..) بیان شده باشند. | |
| رویکرد مفهومی | رویکردهای مفهومی (علت-معلول، دلیل- مدلول و انرژی – نیرو) استفاده شده یکسان نباشد. | |
| سطح عام بودن | سطح عام بودن مفاهیم مورد استفاده در الگوها متفاوت باشد. | |
| سطح انتزاع | سطح انتزاع مفاهیم مورد استفاده در الگوها متفاوت باشد. | |
| نگرش | نگرش (پارادایم) الگوها متفاوت باشد. | |
اگر یک سامانه علی را به چند حوزه تقسیم کنیم میتوان هر حوزه را یک جزء در نظر گرفت که بین آنها رابطه علی برقرار است. در این صورت به سامانهای اجمالی میرسیم.
مثال: در گرافهای زیر یک سامانه علی در دو سطح جزییات نمایش داده شده اند:
ممکن است بیش از یک نوع تفاوت بین حوزههای متناظر دو الگوی هم موضوع وجود داشته باشند. (دو حوزه متناظر بیش از یک نوع تفاوت داشته و یا تفاوت بین هر دو حوزه متناظر یک نوع باشد.)
مثال: در شکل زیر 3 الگو با سطح انتزاع متفاوت نمایش داده شده است.
تناظر یک الگو با چند شی اصیل
یک الگو عام، نماینده چندین شی اصیل میباشد. هر چه سطح عام بودن افزایش یابد، الگو نماینده شیهای بیشتری خواهد بود.
تناظر الگو با حوزهای از شی اصیل (حوزهبندی شی اصیل)
معمولا نمیتوان یا لازم نیست که الگوی کل یک شی را بدست آورد. به عبارت دیگر حوزههای یک شی که کل شی را پوشش داده و ساخت الگوی هر حوزه که کل حوزه را شامل شود، غیر ممکن یا غیر لازم است. بنابراین الگو (کل شی یا حوزهای از آن) تقلیل یافته50 است.
تقلیل یافته یعنی: الگو شامل همه اجزاء و روابط شی اصیل نیست. تقلیل را میتوان با حذف روابط تعریف کرد. اگر برخی روابط یک سامانه را حذف کنیم، یک زیر سامانه تقلیل یافته حاصل میشود. اگر تمامی روابط یک جزء با سایر اجزاء حذف شوند، آن جزء حذف میشود. (حذف یک جزء مصداقی از حذف رابطه میباشد.)
مثال: در الگوهای زیر از راست به چپ تقلیل یافتگی افزایش مییابد.
نباید تقلیل با اجمال اشتباه شود. هر چند برخی از اجزاء شی اصیل یا الگوی تفصیلی به طور مستقل در الگوی اجمالی نیستند، اما در الگوی اجمالی لحاظ شدهاند. (به عبارت دیگر در الگوی اجمالی، اجزایی وجود دارند که متناظر با چند جزء از شی اصیل یا الگوی تفصیلی میباشند) اما برخی از اجزاء شی اصیل در تقلیل حذف میشوند.
نقش اثباتی یا هنجاری الگو
یک الگو دو نقش ممکن است داشته باشد: اثباتی51، هنجاری52
اگر الگو، شی اصیلی را که در یک زمان (گذشته، حال، آینده) واقعیت دارد توصیف کند، نقش اثباتی دارد.
اگر الگو، شیای را که باید واقع شود را توصیف کند، نقش هنجاری دارد.
در الگوی هنجاری مفهوم باید وجود دارد که نباید با مفهوم ارزش اشتباه شود. حالتهای مختلف یک شی، ارزشهای مختلفی دارند. اگر شیای در حالت مطلوب باشد (حالت واقعی آن بر حالت مطلوب منطبق باشد)، باید مطرح نمیشود. اما اگر حالت شی مسئله باشد (حالت واقعی با حالت مطلوب متفاوت باشد)، الگویی هنجاری طراحی میشود تا مبتنی برآن حالت مورد نظر واقع شود.
نسبت بین الگوها
بین الگوها نسبتهای مختلفی ممکن است برقرار باشد. مثلاً: اشتراک، زیر سامانه(برشی، لایهای، ناحیهای، بعدی)، عام-خاص، تفصیل-اجمال، کل- جزء و …
نسبت بین الگوها تناظر یک به یک با نسبت بین حوزههای مربوطه در شی اصیل ندارد:
هر نسبتی بین الگوها باشد، همان نسبت بین حوزههای مربوطه برقرارمیباشد. برای مثال اگر دو الگو با هم اشتراک داشته باشند، حوزههای مربوطه هم اشتراک دارند.
هر نسبتی بین حوزهها باشد، لزوماً آن نسبت بین الگوهای آن حوزهها برقرار نیست. برای مثال ممکن است دو حوزه با هم اشتراک داشته باشند اما الگوهای آنها با تقلیل صورت گرفته، با هم اشتراک نداشته باشند.
انواع روابط بین مصادیق دو حوزه در ماتریس زیر آمده است:

تطابق الگو با شی اصیل
در نظریه الگوی علی، با فرض وجود رابطههای علی در جهان خارج از ذهن، تلاش میکنیم تا این رابطهها را شناسایی کنیم. در طراحی یک الگو به چند شی نقشهای علت و معلول را نسبت میدهیم و با این نسبت از مفاهیم و گزارههای الگوی علی استفاده مینماییم. برای تطابق الگوها شی اصیل باید درستی نقشهای علی که به اشیاء نسبت داده ایم، اثبات گردد. البته قبل از استفاده از الگوی علی باید قانون علیت که وجود رابطه علی را مطرح میکند، اثبات گردد. (دقت شود که نظریه الگوی علی متمایز از نظریه علیت بوده و نظریه الگوی علی با فرض صحت قانون علیت قابل طرح میباشد).
اعتبار الگو
قانون علیت
طبق قانون علیت: «هیچ تغییری بدون علت نیست.» عبارت دیگر «تغییر تصادفی محال است.»
تردید در قانون علیت دو علت دارد:
درک نادرست از مفهوم تصادفی بودن. فرض تصادفی بودن در مواردی که نمیتوانیم یا نمیخواهیم سامانه علی را شناسایی کنیم به کار میرود.
عدم امکان پیشبینی: عدم در امکان پیشبینی قطعی به دلیل عدم توانایی در شناسایی سامانه علی و اختیار (اشیایی مانند انسان که مشمول جبر نیستند) میباشد.
مثال: ریختن تاس مشهورترین مصداق روش تصادفی است. به لحاظ نظری میتوان از نحوه ریختن تاس، شرایط محیطی، مشخصات تاس، گرانش زمین و… عدد که میآید را تعیین کرد، اما چون این متغیرها معمولا قابل کنترل نیستند، فرد نمیتواند همواره نتیجه را پیشبینی کند و یا طوری تاس را بیندازد که عدد دلخواه بیاید. یک مثال سادهتر «ده، بیست، سی، چهل» است اگر بین دو نفر این کار انجام شود کاملاً مشخص است که «صد» به کسی میافتد که «ده» از او شروع نشده. اما وقتی تعداد افراد زیاد شود محاسبه این که «صد» به چه کسی خواهد افتاد سخت میشود (مگر اینکه فرد قبلاً محاسبات را انجام داده باشد) بنابراین از «ده، بیست، سی، چهل» کدامیک روش تصادفی استفاده میشود. البته ممکن است انسان در انتخاب گزینه به جای تعقل از روشهای تصادفی استفاده نماید. (مثلا برای انجام کاری قرعه کشی شود) اما در این حالت نیز از محدوده قانون علیِت خارج نمیشود. علم احتمال برای کمک به مواردی است که میخواهیم بدون شناسایی سامانه علی، استنتاجهای قابل اتکایی داشته باشیم. با رویکرد عمل گرایی (پراگماتیسم) میتوان گفت حتی اگر قانون علیت درست نباشد، (به فرض محال) باز هم به دلیل مفید بودن استفاده است.
پی نوشت ها:
↑ [1] شهودی میتوان
↑ [2] چگونگی تمایز بین تغییری که در یک شیء ایجاد میشود با تغییری که باعث به وجود آمدن شیای جدید میگردد، یکی از سؤالهای کهن فلسفی است. با توجه به این که در نظر گرفتن قسمتی از جهان خارج از ذهن به عنوان یک شیء، انتزاع ذهن است؛ یک جواب برای سؤال فوق، میتواند این باشد: «هنگامی که یک تغییر باعث ظهور(Emergence) یک عامل (Agent) جدید میشود، یک شیء جدید پدید آمده است.» (عامل نمایانگر یک عمل است.)
↑ [3] Causal
↑ [4] رابطه همبستگی بین فراوانی حالتهای مصادیق دو شی عام برقرار است.
↑ [5] Effect
↑ [6] Cause
↑ [7] Actor ) Agent )
↑ [8] توضیح کامل این مفاهیم در مفهوم نامه آمده است.
↑ [9] Energy
↑ [10] Force
↑ [11] Work
↑ [12] تعاریف انرژی، کار و نیرو در علم فیزیک عبارتند از: انرژی: توانایی انجام کار. کار: هنگامی که یک نیرو شی را حرکت در میآورد کار انجام میشود. نیرو باعث تغییر اندازه حرکت یک شی میشود.
↑ [13] Unit
↑ [14] یکای کار وانرژی در دستگاه SI «ژول» میباشد.
↑ [15] Power
↑ [16] Rate
↑ [17] Action
↑ [18] Event
↑ [19] Actor, Agent
↑ [20] Process
↑ [21] Behavior
↑ [22] Resource
↑ [23] Waste
↑ [24] Reason
↑ [25] Policy
↑ [26] Causal System
↑ [27] Object
↑ [28] سامانه از عامترین مفاهیمی است که میتوان هر شیء را مصداق آن دانست. جهان (به عنوان یک شیء کل) یک مصداق از مفهوم سامانه است. یکی از انواع روابط بین اشیاء جهان، روابط علّی میباشد. مجموعه اجزاءجهان با روابط علّی بین آنها، سامانه علّی جهانی را تشکیل میدهند
↑ [29] تعیین تابع ارزش در موارد تناقض در نظریه رهیافت بررسی میشود.
↑ [30] رفتار توالی زمانی حالتهای یک شی میباشد.
↑ [31] Language
↑ [32] زبان سامانهای از نمادها است که کارکرد اصلی آن، انتقال اطلاعات میباشد.
↑ [33] برای اطلاع از همه خطمشیها به نظریه فراعلم مراجعه کنید.
↑ [34] یکی از ابهامهای مفهومی در ذهن اکثر افراد، تمایز بین مفهوم «سامانه» و «شبکه» است. شبکه یکی از مفاهیم نظریه گراف و سامانه اصلیترین مفهوم نظریه سامانه است. اگر یک سامانه را با زبان گراف مشخص شود، گراف حاصل، یک شبکه است.
↑ [35] Discrete
↑ [36] Reduced
↑ [37] تقلیل در ساخت هر الگویی رخ میدهد. با زبان گراف، الگویی گسسته از شی اصیل حاصل میشود.
↑ [38] State transition diagram or state chart diagram
↑ [39] الگوی رفتار علی، ماشین متناهی حالت (or finite automaton(FSM) Finite State Machine) نیز نامیده میشود. ماشینهای متناهی حالت در حوزه نظریه ماشینها (Automata theory ) قرار دارند.
↑ [40] برای رسیدن به دوگان هر گراف، نقش کمانها و گرهها جابه جا میشود.
↑ [41] Geometric place
↑ [42] Matrix
↑ [43] معادلات آماری دارای یک جزء تصادفی هستند.
↑ [44] Time series
↑ [45] به عبارت دیگر صحت یک گزارهی ارزش (هنجاری) از صحت گزارههای ارزشی مرتبهی بالاتر و گزارههای علی که رابطهی بین علت و معلول را بیان میکنند استنتاج میشود.
↑ [46] Transitive
↑ [47] مصادیق یک شی عام، ممکن است مقطعی(چند فرد) یا طولی (حالتهای یک شی در طول زمان) باشد.
↑ [48] Circuit
↑ [49] Vicious Cycle of Poverty
↑ [50] Reduced
↑ [51] Positive
↑ [52] Normative